Explaining and Harnessing Adversarial Examples

16 May 2018

TL;DR

DNNによる識別は微小な摂動が加えられることで，識別結果が変わってしまう
Logistic回帰のような単純なモデルは，ノイズに弱いため↑は直感的にわかる
しかし，DNNの場合はそういったノイズにはロバストであるはずである
これは，DNNの演算は基本的に線形であることに由来している
摂動に対して，ロバストにするように正則化項をLossに加えることで汎化性能を向上させることが可能(Adversarial Training)

摂動によって識別結果が変わってしまう

機械学習では本来，

$f(x) \simeq f(x + \eta)$

となるように，学習過程が設計されている．($\eta$は微小なノイズ)
しかし，こうならないような摂動$\eta$を生成することが可能である．
これが，Adversarial Examplesである．
これを改善するのが，Adversarial Trainingである．
Adversarial Trainingはデータポイント$x$の周辺において，識別器の出力を滑らかにするような役割を担う．

線形モデルでの説明

従来研究では，DNNが摂動に弱いのは非線形性と過学習が原因とされていた．
Goodfellowは，入力データが高次元であれば簡単な線形モデルでもこの現象が起きると主張．
摂動を$ \eta $，入力を$ x $としたときに，摂動を加えられた入力 $\hat{x} = x + \eta $をモデルに入力すると出力は

$w^T \hat{x} = w^T x + w^T \eta$

このとき，$ \eta = \epsilon sign(w)$，$ |\eta|_{\infty} = \epsilon$ とすると

$w^T \eta = \epsilon mn$

$n$は$w$の次元数であり，$m$は$w$の平均である．
つまり，$\eta$は$w$の次元数に対して線形性を持っている．言い換えると，入力が高次元になるほど$ w^T \eta $は大きくなり，モデルの出力が大きく変わることを意味する．

DNNで考えると

DNNは通常，非線形関数であるといわれている．非線形関数であるからこそ線形モデルでは解けないタスクを解決できているはずである．
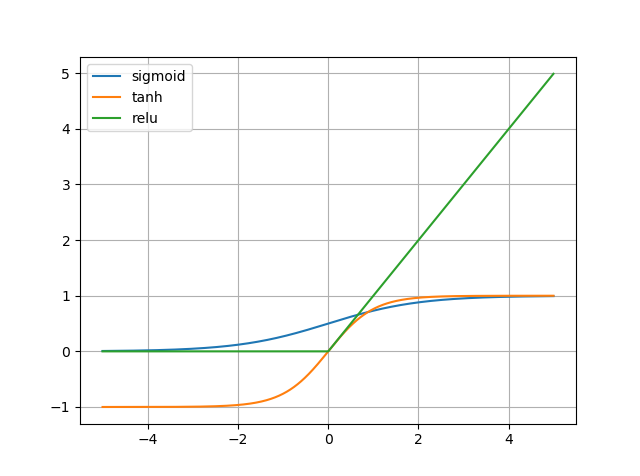
しかし，最近のDNNでは活性化関数として，reluが広く用いられる．
reluは非線形関数であるが，$ x > 0 $においては線形であるため部分線形関数である．
そのため，上の節で述べたような摂動に対して脆弱であるといえる．
tanhやsigmoidなどの非線形関数を活性化として適用することで，これは緩和されるかもしれないが，勾配消失問題が起きてしまうためDNNの活性化関数として，それらを使うことは望ましくない．

Adversarial Training

GoodfellowらはLossに正則化項を加える手法を提案している．
本来のLossを$J(\theta,x,y)$と定義すると，新しいLoss $\hat{J}$は以下になる

$\hat{J}(\theta, x, y) = \alpha J(\theta, x, y) + (1 - \alpha)J(\theta, \hat{x}, y)$ $\hat{x} = x + \eta = x + \epsilon sign(\nabla_xJ(\theta, x, y))$

論文内では，$\alpha = 0.5 $で固定した．
MNISTにおいて，汎化性能の向上を確認．

正則化なしと比べて，文字全体ではなく局所的な特徴をとらえることができている．