1. どんなもの？

• 生成モデルVAEに根拠性を追加したモデル
• その根拠を利用することで異常検知可能
• Disentangleな生成を可能にするLossも同時に提案

2. 先行研究と比べてどこがすごい？

• VAEのような生成モデルでLatent Vectorに根拠性を持たせることはできなかった
• VAEのADモデルでは再構成誤差ベースだったが，本手法のAttention Mapのほうが高精度にADできる

3. 技術や手法の"キモ"はどこ？

Generating VAE Attention

• EncoderのFeature Map $A \in \R^{n \times h \times w}$でlatent vector $z \in \R^d$を微分+GAPすることでvector $\alpha \in \R^n$を求める

$$ \alpha_k = \frac{1}{T} \sum^h_{p=1}\sum^w_{q=1} \frac{\partial z_i}{\partial A^{pq}_k} $$

• $\alpha$と$A$をチャネル毎にinner productしてReLUして，Attention Map $M$を算出($d$ channel分のMapを生成)

$$ M^i = ReLU(\sum^n _ {k=1}\alpha _ k A _ k) $$

• channel方向に平均とって，最終的なAttention Mapとする $$ M = \frac{1}{D} \sum^D_i M^i $$

Generating Anomaly Attention Explanations

• 訓練データ（正常データ）$x$全てから全体の平均ベクトル$\mu_x$と分散ベクトル$\sigma_y$を算出
• テストデータ$y$から，Encoder使って$\mu_y$と$\sigma_y$を算出
• $x$と$y$のnormal difference distributionを定義

$$ P_{q\left(z_{i} \mid x\right)-q\left(z_{i} \mid y\right)}(u)=\frac{e^{-\left[u-\left(\mu_{i}^{x}-\mu_{i}^{y}\right)\right]^{2} /\left[2\left(\left(\sigma_{i}^{x}\right)^{2}+\left(\sigma_{i}^{y}\right)^{2}\right)\right]}}{\sqrt{2 \pi\left(\left(\sigma_{i}^{x}\right)^{2}+\left(\sigma_{i}^{y}\right)^{2}\right)}} $$

• この分布から新たなlatent vectorを生成して，↑のAttentionの枠組みの$z$に代入
  • 式中の$u$は説明がないが，恐らく$u \sim \mathcal{N}(o, I)$

4. どうやって有効だと検証した？

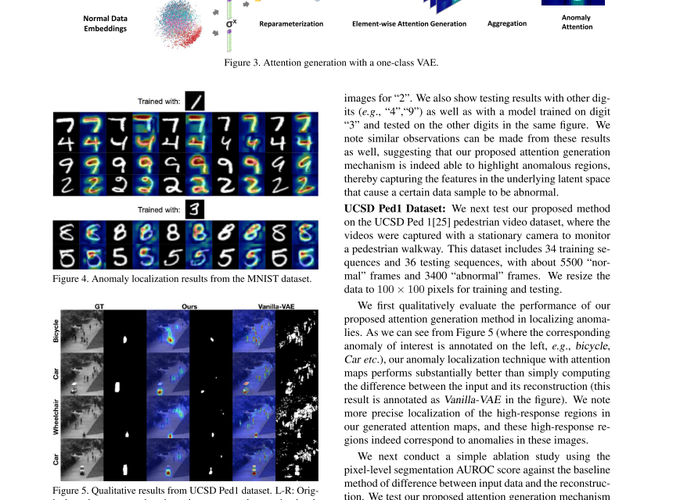
• MNISTで実験

• UCSD Ped1で実験

  • 2回目のDownsamplingのFeature Mapを用いるのがよさそう

• MVTec ADで実験

5. 議論はあるか？

• Fig 3が入力が"5"なのになぜ出力が"9" ?
• $u$ の記述が終始無し
• 公式実行待ち
• Disentangleは気が向いたら

6. 次に読むべき論文はある？