1. どんなもの?
- Patchで学習したCNNをOriginalに対して,sliding windowして特徴抽出する枠組みの改善
- ↑は計算が冗長で計算時間が長い
- Patchで学習したCNNを再学習することなく,pooling layerを置き換えるだけでOK
2. 先行研究と比べてどこがすごい?
- 大きい画像に対して,sliding windowして特徴抽出する方法は計算が冗長で計算時間が長い
- sliding window使わない方法では,poolingやstride などで特徴抽出された画像は元画像よりかなり小さくなる
- e.g.) VGGの場合は,224x224 -> 7x7で1/32のサイズになる
- sliding window使わない方法では,poolingやstride などで特徴抽出された画像は元画像よりかなり小さくなる
- Patchで学習したCNNを再学習することなく,pooling layerを置き換えるだけでOK

3. 技術や手法の"キモ"はどこ?
- 変数の定義
- $I \in \R^{I_h \times I_w \times I_c}$ : Originalの入力画像
- $P_{x, y} \in \R^{P_h \times P_w \times I_c}$ : 位置$(x,y)$のパッチ
- $O_{x, y} = C_p(P_{x, y}) \in \R^{k}$ : 位置$(x,y)$のパッチを通常のCNN $C_p$でfeature extractして得られたベクトル
- $O \in \R^{I_h \times I_w \times I_c}$ :
sliding windowせず,$O \in \R^{I_h \times I_w \times I_c}$ が得られるモデル$C_L$を求めたい
Layers without pooling
- poolingやstride convでないlayerは,Patchで学習したCNNを転用する
Multipool to consider all locations
- Pooling LayerをMultipoolに置き換え
- 2x2のPoolingでは↓のように4つのPooling Patternが考えられる

$$ \operatorname{Pool}_{s \times s}^{x, y}(I)=\operatorname{Pool} _ {s \times s}\left(\operatorname{SHIF} T _ {y, x}(I)\right) $$
Layerの出力は4つのPooling Patternの出力の集合.
通常Poolingすると,解像度が落ちるがこの方法では落ちていない.
$$ L _ {I}^{\text {multipool}}=\{\text {Pool} _ {s \times s}^{0,0}, \text {Pool} _ {s \times s}^{0,1}, \ldots, \text {Pool} _ {s \times s}^{0, s-1}, \ldots, \text {Pool} _ {s \times s}^{s-1,0}, \ldots, \operatorname{Pool} _ {s \times s}^{s-1, s-1}\} $$
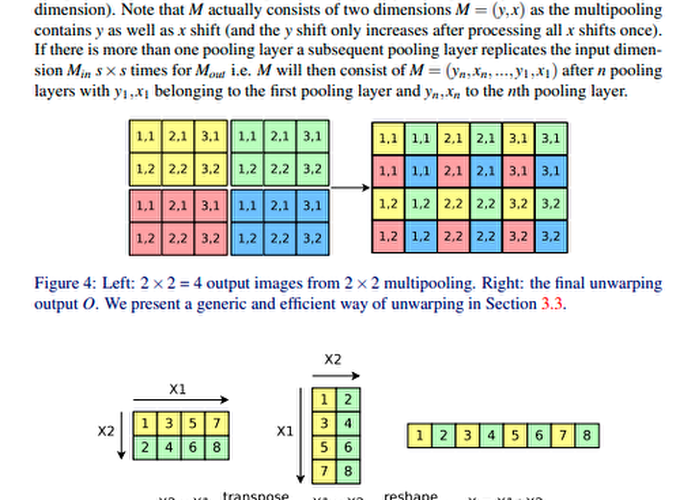
Unwarping
-
1個のMultipoolを持つCNNの出力は,Leftであり,それを並べ替えてRightにする

-
演算的には,(Leftのshape:$(s=2, s=2, \frac{I_h=4}{s=2}, \frac{I_w=6}{s=2}, k=1)$)
- transpose dim=(1, 2) -> (2, 2, 2, 3, 1)
- reshape (2x2, 2x3, 1) -> (4, 6, 1)
-
$n$個のMultipoolを持つ場合は,出力のshapeは$(s^n, s^n, \frac{I_h}{s^n}, \frac{I_w}{s^n}, k)$
-
loop
for i in range(0, n)- reshape -> $(s^{n-i}, s^{n-i}, \frac{I_h}{s^{n-i}}, \frac{I_w}{s^{n-i}}, k)$
- transpose dim=(1, 2) -> $(s^{n-i}, \frac{I_w}{s^{n-i}}, s^{n-i}, \frac{I_h}{s^{n-i}}, k)$
-
reshape -> $(I_h, I_h, k)$
-
※ 論文内の記述を理解できなかったので,プログラムの方から解釈してます↑
4. どうやって有効だと検証した?
GTX TITAN Xを使って,sliding windowと速度比較

5. 議論はあるか?
- Unwarpingの式の記述の仕方が理解できなかった
- Githubのプログラムはこれであってるのか?
- reshapeとtranspose周り