1. どんなもの?
- SVMの距離をユークリッド空間ではなく,非ユークリッド空間で取る
- 具体的にはPoincare disk上とか
2. 先行研究と比べてどこがすごい?
- SVMの距離算出を比ユークリッド空間で行う
- 階層構造を持つデータなどに対して精度良く識別ができる
- textとかgraphとか
3. 技術や手法の"キモ"はどこ?
前提知識
Hyperbolid model
- 内積が$x*y = x_0y_0 - x_1y_2 - \cdots x_ny_n$で定義されるMinkowski space
- $n$次元のhyperbolid model $\mathbb{L_n}$は$\mathbb{R} ^ {n+1}$の単位球の上半平面上にある
$$
\mathbb{L}^{n}=\left \{ x: x=\left(x_{0}, \ldots, x_{n}\right) \in \mathbb{R}^{n+1}, x * x=1, x_{0}>0\right \}
$$

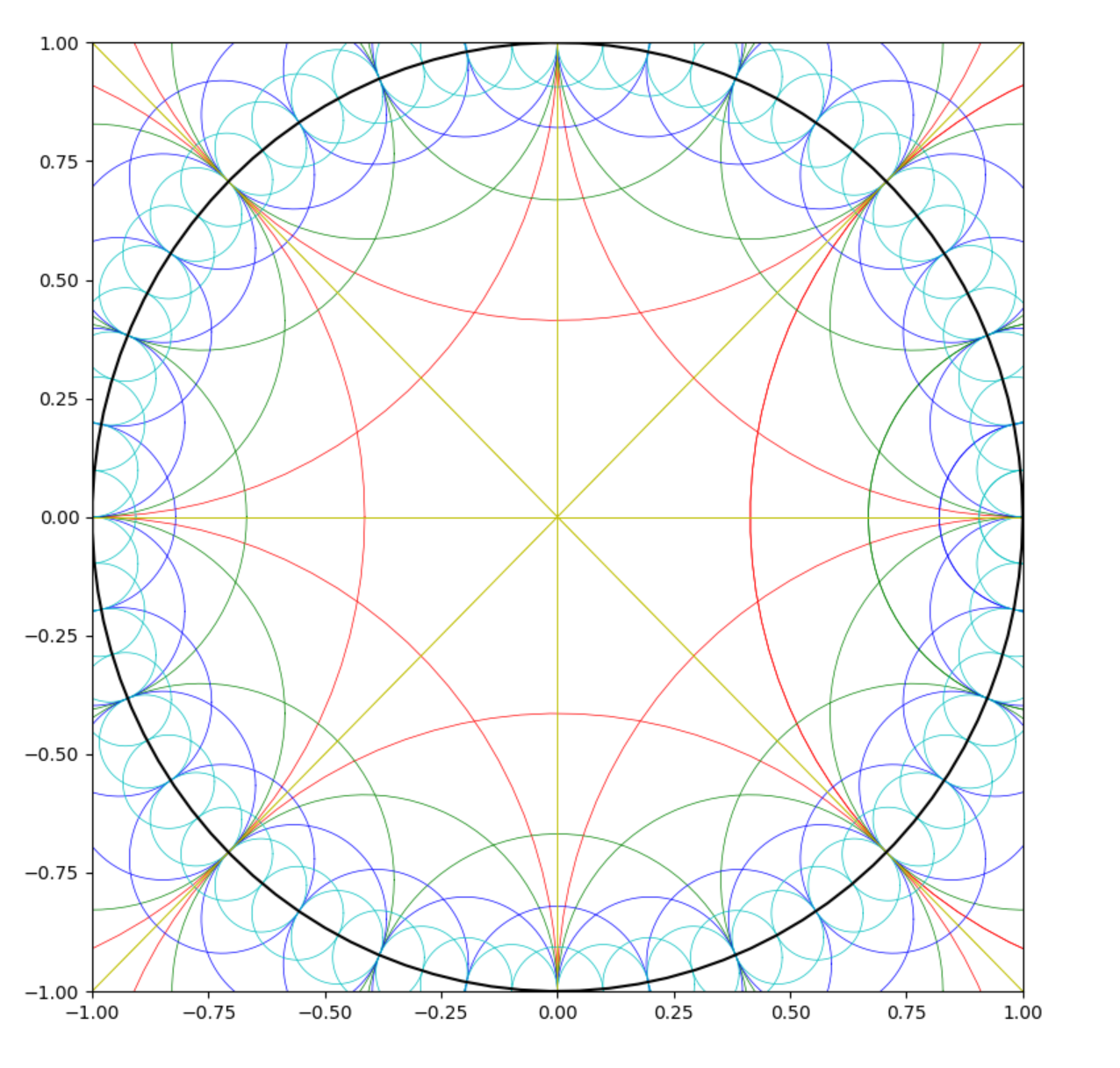
Poincare Ball
- 有名なポアンカレ円盤 $$ \mathbb{B}^{n}=\left \{ x: x=\left(x_{1}, \ldots, x_{n}\right) \in \mathbb{R}^{n},|x|^{2}<1\right \} $$
- hyperbolidの特殊な形と言える
$$
\left(x_{0}, \ldots, x_{n}\right) \in \mathbb{L}^{n} \Leftrightarrow\left(\frac{x_{1}}{1+x_{0}}, \ldots, \frac{x_{n}}{1+x_{0}}\right) \in \mathbb{B}^{n}
$$

SVM
- 目的関数は $$ \operatorname{minimize} _ {w \in \mathbb{R} ^ {n}} \frac{1}{2}|w|^{2}+C \sum_{j=1}^{m} \max \left(0,1-y^{(j)}\left(w^{T} x^{(j)}\right)\right) $$
Hyperbolic Support Vector Classification
- $x$からdecision boundaryまでの距離を下で定義 $$ \sinh ^{-1}\left(\frac{w * x}{\sqrt{-w * w}}\right) $$
- 目的関数は $$ \operatorname{minimize} _ {w \in \mathbb{R}^{n+1}}-\frac{1}{2} w * w+C \sum_{j=1}^{m} \max \left(0, \sinh ^{-1}(1)-\sinh ^{-1}\left(y^{(j)}\left(w * x^{(j)}\right)\right)\right) $$ $$ \text{subject to } w * w<0 $$
4. どうやって有効だと検証した?
- GMM(混合数4)から発生させたデータに対して実験

- 4つのreal datasetに対して実験
- 生で使うのではなく,embdして識別
- 比較がずるい気がする

5. 議論はあるか?
- 精度云々は置いておいて,距離を非ユークリッド空間でとるアイデア
6. 次に読むべき論文はある?
- https://tech-blog.abeja.asia/entry/poincare-embeddings
- https://tech-blog.abeja.asia/entry/hyperbolic_ml_2019
- Nickel, M., & Kiela, D. (2018). Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry. Retrieved from http://arxiv.org/abs/1806.03417